Wie du sicherlich bereits weißt, haben elementare Stoffe gleichviele Elektronen und Protonen. Die Protonenzahl ist gleichzeitig die Kernladung und die Ordnungszahl und bestimmt damit das Element. Für Hauptgruppenelemente gilt deshalb wie in der Grafik veranschaulicht, dass ein zusätzliches Elektron mit einem zusätzlichen Proton einhergeht, sodass sich die Ladungen ausgleichen.


Die Anzahl an Elektronen kann sich bei Kationen oder Anionen aber vom ungeladenen Zustand des Atoms unterscheiden, was sich auf das chemische Verhalten auswirkt. Atome desselben Elements haben immer dieselbe Anzahl an Protonen, aber müssen nicht gleichviele Neutronen haben. Das wirkt sich auf die Masse und andere physikalischen Eigenschaften aus. Eisen beispielsweise hat 26 Protonen und Elektronen und ist bei einer Massenzahl von 56 bis 58 stabil, also bei 30 bis 32 Neutronen. Die Massenzahl ist die Summe der Nukleonen (Nukleonen sind Protonen und Neutronen) und nicht zu verwechseln mit der Atommasse. Die Atommasse lässt sich zwar gut an die Masse des Atomkerns annähern, aber da Protonen und Neutronen unterschiedliche Massen haben, ist bei unterschiedlichen Verhältnissen der Nukleonen die Atomkernmasse kein einheitliches Vielfaches der Massenzahl. Obwohl Eisen nur zwei stabile Isotope hat (was ein Isotop ist, klären wir gleich), kann es trotzdem 20 bis zu 39 Neutronen haben. Bei weniger als 30 und mehr als 32 Neutronen ist Eisen aber instabil, weshalb es radioaktiv zerfällt. Weil die Anzahl an Neutronen trotz desselben Elements unterschiedlich ist, gibt man deshalb die Massenzahl eines Atoms an. Die Massenzahl und die Ordnungszahl beschreiben dabei vollständig ein Nuklid. Nuklide sind Atome, die auf ihren Atomkern reduziert sind. Außerdem reichen die Massenzahl und die Ordnungszahl, um herauszufinden, von welchem Element das Nuklid ein Isotop ist. Isotope sind Nuklide mit gleichvielen Protonen, also Atome desselben Elements, mit unterschiedlich vielen Neutronen. Sogenannte Reinelemente haben dabei ein stabiles Isotop, Mischelemente hingegen bei gerader Kernladungszahl bis zu zehn und bei ungerader Kernladungszahl maximal zwei stabile Isotope.

Isotope haben also die gleiche Ladung, aber unterschiedliche Massen. Deshalb lassen sich die Isotope einer Probe mithilfe der sogenannten Massenspektrometrie voneinander trennen. Unten ist der schematischen Aufbau einer massenspektrometrischen Untersuchung animiert. Dabei wird eine Gasprobe durch das Probeneinlasssystem in eine Hochvakuumröhre eingelassen und anschließend mit freien Elektronen beschossen. Die freien Elektronen kommen aus einer Glühkathode und werden durch eine Beschleunigungsspannung in Richtung der Probe beschleunigt. Dadurch kommt es zur Elektronenstoß-Ionisierung der Teilchen im Gas. Dabei werden Elektronen aus den Teilchen der Probe herausgeschlagen und es entstehen aus dem Teilchen und einem freien Elektron ein Kation und zwei langsame Elektronen. Die Kationen werden dann mithilfe einer Lochanode, also einem Minuspol, durch elektrische Anziehung beschleunigt und in einem Strahl fokussiert. Im Trennrohr wird der Ionenstrahl anschließend im Magnetfeld sortiert, indem die Teilchen abhängig von der Masse und Ladung unterschiedlich stark abgelenkt werden: Die Ablenkung ist proportional zur Ladung und verringert sich bei einer größeren Masse. Schließlich werden sie elektronisch als Ionenströme am Detektor registriert und als Massenspektrum angezeigt. Bei der Massenspektrometrie kann man deshalb Isotopen desselben Elements keine diskrete Ablenkung zuordnen, sondern man erhält mehrere elementspezifische Ablenkungen, die sich bei einer Mischungsprobe, die verschiedene Elemente enthält, teilweise auch mit anderen Elementen überschneiden können. Deshalb summiert man nicht nur die Massen der Nukleonen und Elektronen, sondern relativiert die Masse zu ihrer Ladung:



In der Größenordnung von Molekülen oder Ionen ist die Ladung meistens ein kleines Vielfaches der Elementarladung. Deshalb ist es auch sinnvoll, die Ladung q als Vielfaches der Elementarladung auszudrücken. Mit der Masse lässt sich aber in der Größenordnung schlecht rechnen. Anstelle der Einheit Kilogramm hat man deshalb den Referenzwert der atomaren Massenskala für Kohlenstoff ¹²C bei 12u definiert. U steht dabei für unit, also einfach „Einheit“, und ein u entspricht etwa 1,661*10^-27 kg. Durch die Einführung der atomaren Massenskala entspricht die Massenzahl von ausschließlich ¹²C-Kohlenstoff genau seiner Atommasse.
Bei einer Einstoffprobe werden die relativen Häufigkeiten der Isotope eines Elements nach einer massenspektrometrischen Untersuchung als relative Intensitäten der Ionenströme gemessen. Dadurch ergibt sich eine Isotopenverteilung, aus der man die mittlere Masse des Isotopengemischs als Summe der Produkte aus der Isotopmasse m und der entsprechenden relativen Häufigkeit h berechnen kann:


Bei Proben aus der Natur spricht man von einer natürlichen Isotopenverteilung, die bis auf Blei für alle Elemente näherungsweise auf der gesamten Erde gleich ist. Allerdings ändern sich bei radioaktiven Elementen selbst die natürlichen Isotopenhäufigkeiten, weil einige Isotope eher zum radioaktiven Zerfall tendieren und so die Häufigkeit derjenigen Isotope schneller abnimmt, die instabiler sind, einfach, weil sie mit der Zeit schneller zerfallen als stabile Isotope.

Mit der Massenspektrometrie lassen sich bei einer Mehrstoffprobe auch die Elemente bestimmen, aus denen die Probe besteht. Aus den Masseanteilen, die der prozentualen Elementarzusammensetzung entsprechen, kann man dann auf die Substanzformel schließen, die auch empirische Formel genannt wird. Man sollte dabei klar zwischen der Substanzformel und der Molekülformel unterscheiden: Die Substanzformel ist nämlich das Stoffmengenverhältnis der Bestandteile und man rundet auf die kleinste stöchiometrische Zahl. Bei Kohlenstoffdioxid CO₂ beispielsweise ist das Stoffmengenverhältnis zwei Teilchen Sauerstoff auf ein Teilchen Kohlenstoff. Die Molekülformel allerdings gibt die tatsächliche Anzahl an Atomen eines Elements in einer molekularen Verbindung an. Beim Kohlenstoffdioxid sind Substanz- und Molekülformel identisch, da jedes Molekül aus einem Kohlenstoff- und zwei Sauerstoffatomen besteht und die stöchiometrischen Zahlen nicht weiter gekürzt werden können. In der organischen Chemie wie beim Alken Ethen zum Beispiel macht es allerdings einen sehr großen Unterschied. Die Molekülformel ist C₂H₄, weil das Molekül aus zwei Kohlenstoff- und vier Wasserstoffatomen besteht. Wenn man aber die kleinsten stöchiometrischen Zahlen für die Substanzformel ermitteln will, kann man hier ganz gut kürzen und erhält die Substanzformel CH₂, was aber Methylen entspricht.
Für die Rechnungen später benötigen wir einige grundlegende Formeln, die sehr einfach sind und die du dir nun merken solltest:

1. Um besser mit Atommassen rechnen zu können, werden Atome zu einem Mol zusammengefasst, was 6,022*10²³ Teilchen entspricht. Diese Zahl wird als Avogadro-Konstante bezeichnet und entspricht allgemein den Teilchen pro Stoffmenge: . Mit dieser Konstante rechnest du zwischen der makroskopischen Ebene eines Mols und der atomistischen Ebene eines einzelnen Teilchens um.
2. Abgesehen davon entspricht die Masse eines Mols Teilchen in Gramm genau der atomaren Masse in u. Dementsprechend gilt für diese sogenannte molare Masse dieser Zusammenhang: .
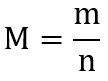3. Der dritte, sehr grundlegende Zusammenhang, den du häufig verwenden wirst, ist die Konzentration c, die die Stoffmenge n eines Volumens V beschreibt: .

 
Die Verbindung von Protonen und Neutronen zu einem Kern erfordert erst Energie, die wegen der Coulomb-Abstoßung, also der abstoßenden elektrischen Kraft, exponentiell zunimmt. Ab einem bestimmten Abstand fällt die Energie aber sprunghaft, weil der Kern gebunden stabiler als seine einzelnen Bestandteile ist. Nach Albert Einsteins spezieller Relativitätstheorie sind Masse und Energie proportional zueinander, das heißt der Kern wiegt physikalisch betrachtet auch weniger als die Summe der Massen der Nukleonen, weil die Energie sinkt. Die Energiedifferenz bewirkt deshalb einen Massendefekt, der sich aus der Differenz zwischen der berechneten Masse und der gemessenen ergibt:


Die Masse ergibt sich rechnerisch aus der Gesamtmasse der Nukleonen. Für die zerstrahlte Masse, die durch den Massendefekt entsteht, fehlt uns eigentlich nur der Proportionalitätsfaktor zur Energie. Der lässt sich aus der speziellen Relativitätstheorie herleiten:
 

Abhängig von der Zusammensetzung des Kerns gibt es zwischen den Elementen Unterschiede in der Stabilität, weil die elektrische Abstoßung der Protonen sich auf die Kernbindungsenergie auswirkt. Das Energieminimum entspricht dem Stabilitätsmaximum und liegt bei („Eisen-56“) und („Nickel-62“), das heißt bei kleineren Kernen kommt es tendenziell eher zur Kernfusion und bei größeren zur Kernspaltung. Beide Vorgänge setzen Energie frei, wobei die Energieumsätze um sieben Größenordnungen größer als die Energieumsätze chemischer Reaktionen sind. Bei Kernfusion (bekannt z.B: aus der Sonne) und Kerspaltung (wie z.B. in Kerkraftwerken oder Atombomben) werden also gewaltige Energien frei Die Energie wird durch die Anregung von Elektronen und das Zurückspringen in den Grundzustand in Form von elektromagnetischer Strahlung frei.

KLAUSURAUFGABEN

In der Klausur wurde schon einige Male zum Thema Massenspektrometrie danach gefragt, aus einer prozentualen Elementarzusammensetzung auf die Substanzformel zu schließen.

Aufgabe 1: SS 2019, 5. Gegeben war dabei zum Beispiel eine Verbindung aus 86,62% Blei und 13,38% Sauerstoff. Wir interessieren uns für die Substanzformel, also für das Stoffmengenverhältnis . Die Stoffmenge können wir dann jeweils durch beschreiben:

Die molaren Massen lassen sich ganz einfach aus dem Periodensystem in der zweiten Zeile herauslesen. Die Massen ergeben sich aus den Masseanteilen aus der Aufgabenstellung. Es ist nämlich äquivalent zu sagen, dass Blei einen Masseanteil von 86,62% hat oder 86,62g von einer 100g Probe. Diese Werte setzen wir dann in die Formel ein

und erhalten einen Bruch. Dieser Bruch entspricht unserem Stoffmengenverhältnis und gibt uns die stöchiometrischen Zahlen an. In diesem Fall ist das Verhältnis etwa ein Halb, das heißt wir haben zwei Sauerstoffatome auf ein Bleiatom und die Substanzformel ist PbO₂.


Aufgabe 2: SS 2018, 4. Eine andere Verbindung aus 52,93% Aluminium und 47,07% Sauerstoff hat nach derselben Vorgehensweise ein Stoffmengenverhältnis von etwa 2:3

und damit die Substanzformel Al₂O₃.

 
Abgesehen von den Verbindungen, die wir berechnen können, wird auch gerne mal nach einige Verbindungen und Elementvorkommen gefragt, sodass es ratsam ist, diese im Kopf zu haben. Dazu gehören zum einen die Elementvorkommen auf der Erdkruste, im menschlichen Körper und in trockener Luft. Zum anderen müssen wir uns auch einige Verbindungen merken, die du auch im Bild findest. Außerdem werden immer wieder Salze und Säurereste abgefragt, womit du in der Klausur ein paar sichere Punkte sammeln kannst. Schließlich lässt sich noch sagen, dass du unbedingt auch auf die korrekte Schreibweise der Substanzformeln achten solltest, also für Ethanol zum Beispiel nicht C₂H₃OH schreibt, sondern C₂H₄O.